Visual Disabilities
Color-blindness
Types of Color-blindness
Color-blindness or color vision deficiency is the inability to distinguish certain shades of color. It is a fascinating topic because of its complexity. There are three types of photoreceptors within the eye. Each is responsible for detecting different color wavelengths. Additionally, there are photoreceptors that detect light intensity, called rods. Color-blindness can occur if any of these types of photoreceptors is missing or functioning incorrectly. The most common type of color-blindness is red-green deficiency—this doesn't mean that red and/or green cannot be seen, but that certain shades of red and green may be difficult to differentiate.
The key principle of web accessibility for users with color-blindness is:
- Perceivable: the difference between certain color combinations may be difficult to perceive.
The colors with which they have difficulty distinguishing depend upon their type of color-blindness, but red-green deficiencies are the most common.
Red-green deficiencies
Individuals with a red-green deficiency have difficulty distinguishing between some shades of reds and greens, but they can still differentiate between a light color and a dark color. A dark red and a light green will be easy to distinguish because of their contrast difference. People with red-green color-blindness may see reds and greens as yellows, oranges, and beiges. This means that yellows, oranges, and beiges can be confused with greens and reds. Blue is not affected by this type of color blindness.
Protanopia and protanomaly (red deficiencies)
Protanopia and protanomaly occur when the cones in the eye primarily responsible for detecting red are missing or malfunctioning. The greens tend to look similar to the reds. Protanomaly is milder than protanopia, but the result is similar. Many people with protanomaly can distinguish some reds and greens with some difficulty, and, as with protanopia, reds tend to look darker as well.
Normal
Protanopia
Deuteranopia and deuteranomaly (green deficiencies)
Deuteranopia and deuteranomaly occur when the cones primarily responsible for detecting green are missing or malfunctioning, but the end result is very similar to protanopia, with the exception that reds do not appear as dark. Deuteranomaly is the less serious of the two conditions. Individuals with deuteranomaly can often distinguish between the shades of reds and greens relatively accurately.
Normal
Deuteranopia
Other deficiencies
Tritanopia and tritanomaly (blue deficiencies)
Tritanopia and tritanomaly are much less common than the other types. Tritanopia is when the cones primarily responsible for detecting blue are missing or malfunctioning. Blues and greens may appear very similar, and yellows may appear as lighter shades of red or may seem to disappear completely.
Normal
Tritanopia
Rod monochromacy or achromacy (no color)
This group constitutes an extremely small minority among people who are color-blind. All three types of cones or either missing or non-functional, so the rods (the photoreceptors which can only differentiate between light and dark) are the only available source of visual information. Individuals with achromacy see the world as if in grayscale—everything will appear in black, white, and shades of gray. This often results in poor visual acuity and an aversion to bright light.
The term "color-blindness" is most true for this type of deficiency, since these individuals entirely lack the ability to see any color, whereas the color-deficiency is most accurate when people only lack part of the color spectrum.
Normal
Achromacy
Designing for Color-blindness
When designing web content it is not necessary to get rid of color. It is not necessary to convert all images to black and white or get rid of images entirely. In fact, it may not be necessary to change anything at all.
Make sure that colors are not the only method of conveying important information.
Most of the time color is irrelevant in understanding content on the web. However, when colors are used to convey or differentiate information—such as a pie chart or bar graph, or using green and red text to indicate pass/fail or good/bad, etc.—this information should also be provided in another way.
For example, the image below shows a portion of the New York City public transportation system, where the routes are distinguished by the color of the lines.
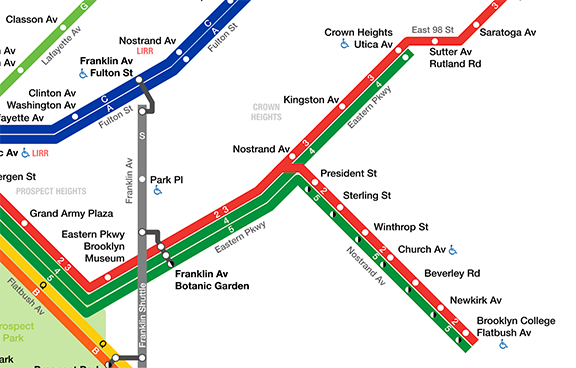
When color information is removed, the routes are very difficult to differentiate.
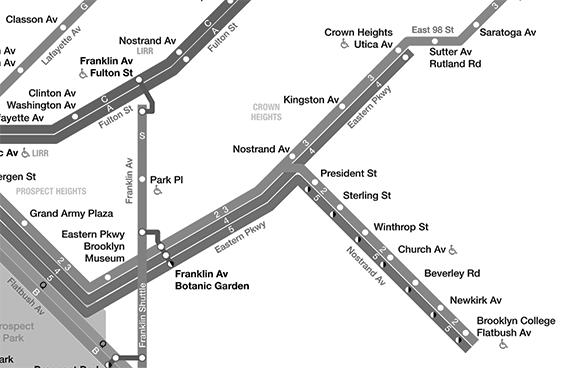
While using the color enhances the user experience, when colors may not be perceived (including by users who are blind), are overridden by custom settings, or are not readily distinguishable this information would need to be conveyed by annotating the image, using different styles for each line, or by supplementing the image with text on the web page that conveys the same information.